Septiembre 96-97, Opción A

1. Explica el concepto de energía potencial eléctrica. ¿Qué energía potencial eléctrica tiene una carga q₁ situada a una distancia r de otra q₂.

2. Dos partículas con igual carga q = 0,1 μ C están fijas en el vacío y separadas una distancia d = 1 m. Otra partícula de carga q’ = 2 μ C, sobre la que sólo actúa el campo eléctrico de las anteriores, se desplaza desde el punto A hasta el B de la figura, situados en el punto medio entre las dos cargas y en el punto que forma un triángulo equilátero con ambas, respectivamente. En el desplazamiento A à B, ¿cuánto variará la energía cinética de q’?.

Constante de Coulomb: K = 1/(4π ε ₀) = 9·10⁹ N·m²·C^-2.

 

1. Energía potencial eléctrica de un sistema es el trabajo, cambiado de signo, que ha realizado el campo electrostático para pasar desde el nivel de referencia de energía potencial (cargas infinitamente alejadas, E_p = 0) hasta la distribución de cargas de ese sistema.

Esta definición, de trabajo realizado por el campo cambiado de signo, nos permite expresar la energía potencial como el trabajo realizado contra el campo (una fuerza idéntica a la ejercida por el campo eléctrico pero de signo opuesto) para obtener la distribución de cargas del sistema, partiendo del nivel de referencia (que usualmente tomamos como cargas infinitamente alejadas).

Así pues, podemos considerar que el trabajo realizado contra el campo se queda almacenado en forma de energía potencial; y que este trabajo nos será devuelto por el campo cuando dejemos evolucionar al sistema en libertad, disminuyendo su energía potencial mediante un trabajo positivo del campo.

Si la energía potencial de un sistema es negativa quiere decir que el propio campo ha realizado el trabajo para conseguir esa distribución de cargas, mientras que nosotros hemos debido hacer un trabajo negativo (si es preciso) para frenar esas cargas que se aproximaban desde el infinito.

Si, por el contrario, la energía potencial de un sistema es positiva, hemos debido hacer un trabajo positivo contra el campo (que lo habrá hecho negativo) para llegar a esa distribución.

En el caso particular de dos cargas puntuales o con simetría esférica, q₁ y q₂, situadas a una distancia r, la interacción entre ellas vendrá dada por la Ley de Coulomb:

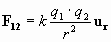
Si calculamos el trabajo realizado por esta F para acercar ambas cargas desde el infinito hasta una distancia r, obtenemos:

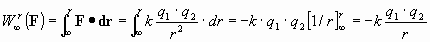
Así pues la energía potencial de ese sistema será, como hemos visto antes:

Si las cargas son del mismo signo la energía potencial será positiva: nos habrá costado trabajo acercarlas hasta esa distancia; y si son de distinto signo la energía potencial será negativa: el campo las habrá acercado.

2. Al actuar sólo el campo eléctrico y ser un campo conservativo, la energía se conservará en todo el desplazamiento y, más concretamente, en los puntos inicial y final del mismo.

Podemos utilizar dicha conservación para calcular la variación de energía cinética, pues si la variación de energía total es 0 al ser constante, debe ocurrir que:

Δ E_C = -Δ E_P

Por tanto, debemos calcular la variación de energía potencial. Para ello, podemos utilizar el concepto de potencial eléctrico en un punto, pues la E_P de la carga q' situada en ese punto se obtiene con:

E_P = q'·V

El problema queda reducido a obtener los potenciales de los puntos A y B.

Para ello, debemos utilizar el principio de superposición y la expresión del potencial creado por una carga puntual.

Al ser dos cargas iguales las que originan el potencial, obtenemos:

Luego:

Δ E_C = 3,6·10^-3 J